黑客的统计学

最近看到一个题为《Statistics for Hackers》(黑客的统计学)的PPT，非常有意思，和大家分享一下。

这儿的Hacker（黑客）并不是是指那些尝试窃取你银行密码的人，而是那些善用编程来解决问题的人。

作者Jake VanderPlas是华盛顿大学的资深数学科学研究员，他在PPT中表示统计学很难，但是使用编程技能后，它也可以很简单，他深圳宣称：只要你会写 for 循环，你就能做统计。

最重要的是： 问正确的问题

1. 热身：抛硬币问题（直接模拟）

问题：你抛一个硬币30次，其中22次正面朝上。问这个硬币是均匀的吗？

这是一个经典的问题。有人认为均匀的硬币抛 30 次应该有 15 次朝上，所以这个硬币不均匀，也有人认为即使是均匀的硬币也有可能因为偶然而抛出 22 次朝上。

经典的解法如下：

假设硬币是均匀的，然后验证这个原假设，计算一个均匀的硬币抛出 22 次正面的概率是多少?

开始计算，如下图所示：

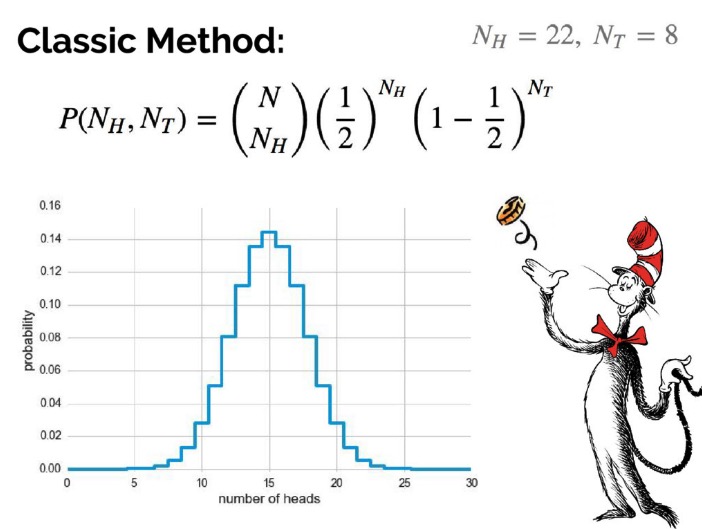
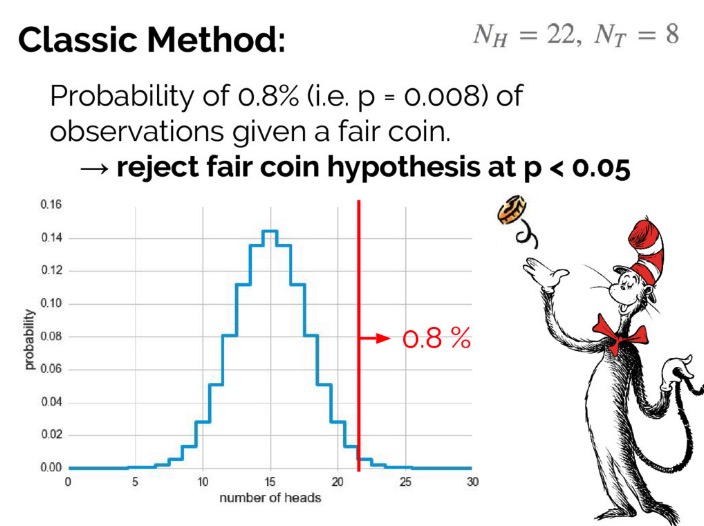
列出公式后，计算得知如果硬币是均匀的，那么抛 30 次并且有 22 次正面朝上的概率是 0.008，或者说如果抛 30 次并且观察到 22 次正面朝上，则这枚硬币是均匀的概率为 0.008。这个 0.008 一般称为 p 值，习惯上，当 p 值小于 0.05（有些时候取 0.01）时，我们认为这件事是不太可能发生的，因此拒绝原假设，即得到结论：硬币不是均匀的。

那么，是否有什么简单的方法呢？

这时，编程方法就可以派上用场了，我们只需要模拟一下：

from random import randint

N = 1000000;
M = 0;
for i in range(N):
	trials = (randint(0, 1) for i in range(30)) 
	if sum(trials) >= 22:
		M += 1
p = M / N #0.00819

结论：由于 p = 0.008，拒绝原假设，硬币不是均匀的。

简单来说，计算样板分别比较困难，但模拟样本分布很简单。

2. 随机打乱

观察两组数据：

★		✖︎
84	72	81	69
57	46	74	61
63	76	56	87
99	91	69	65
		66	44
		62	69

★ 均值：73.5
✖︎ 均值：66.9
差异：6.6

问题来了：两组数据的差异 6.6 是统计显著的吗？

经典解法如下：

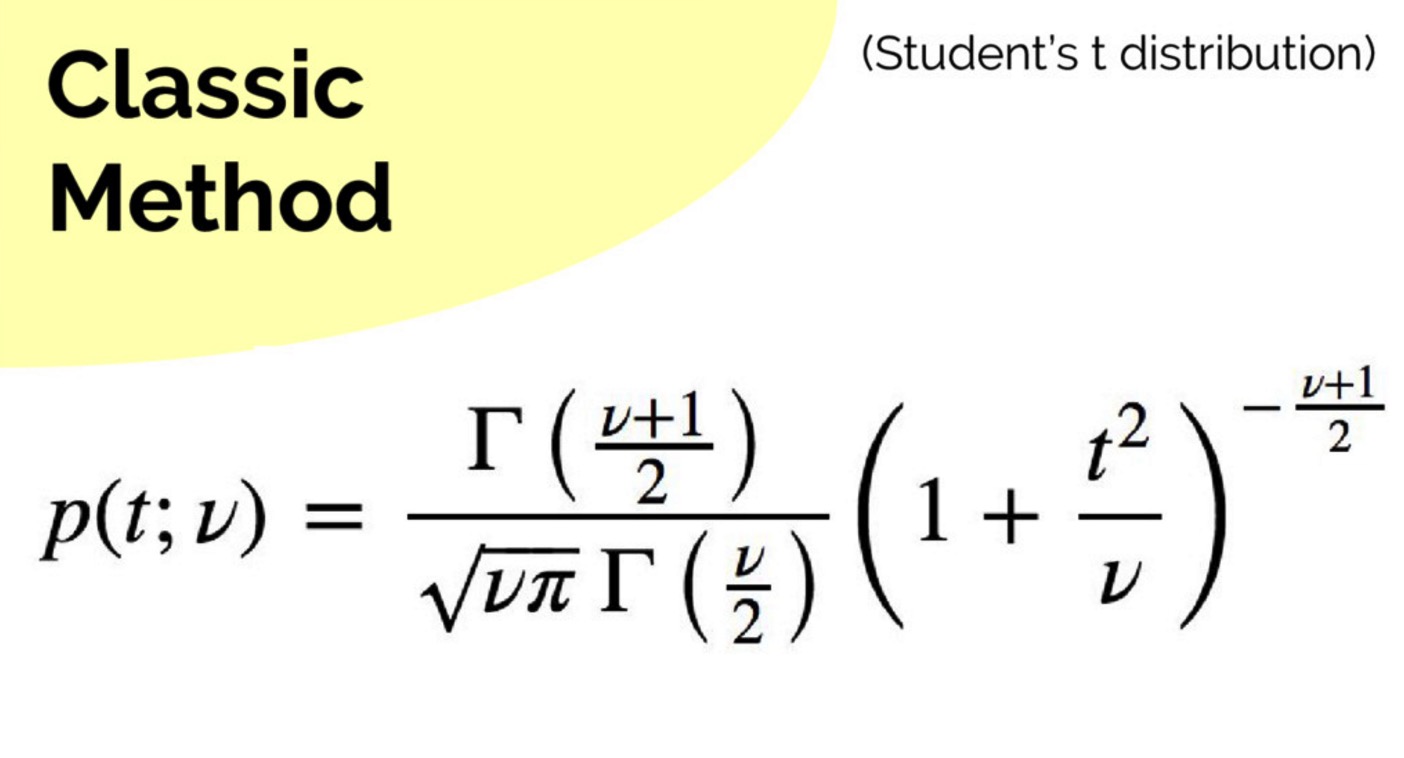
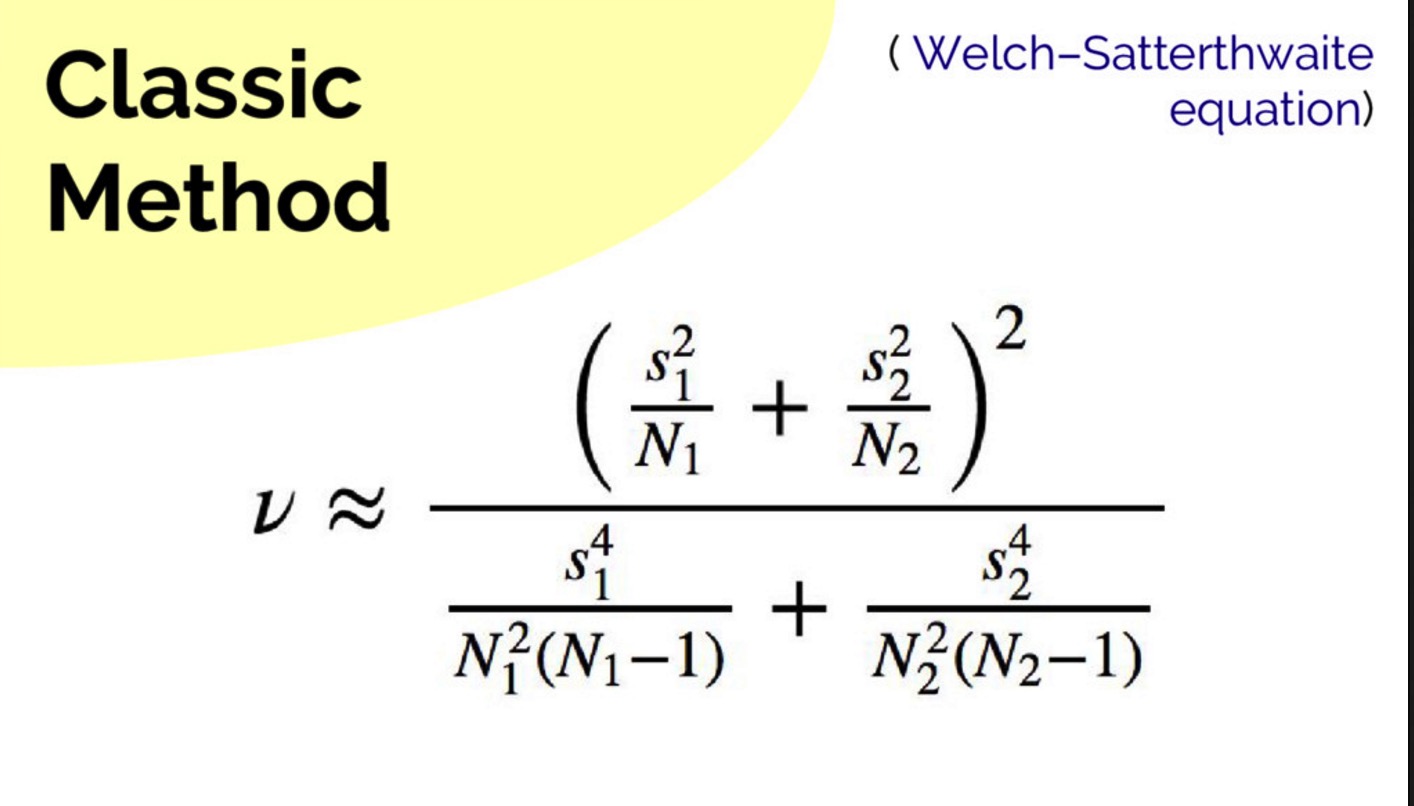
然后查表，可得：

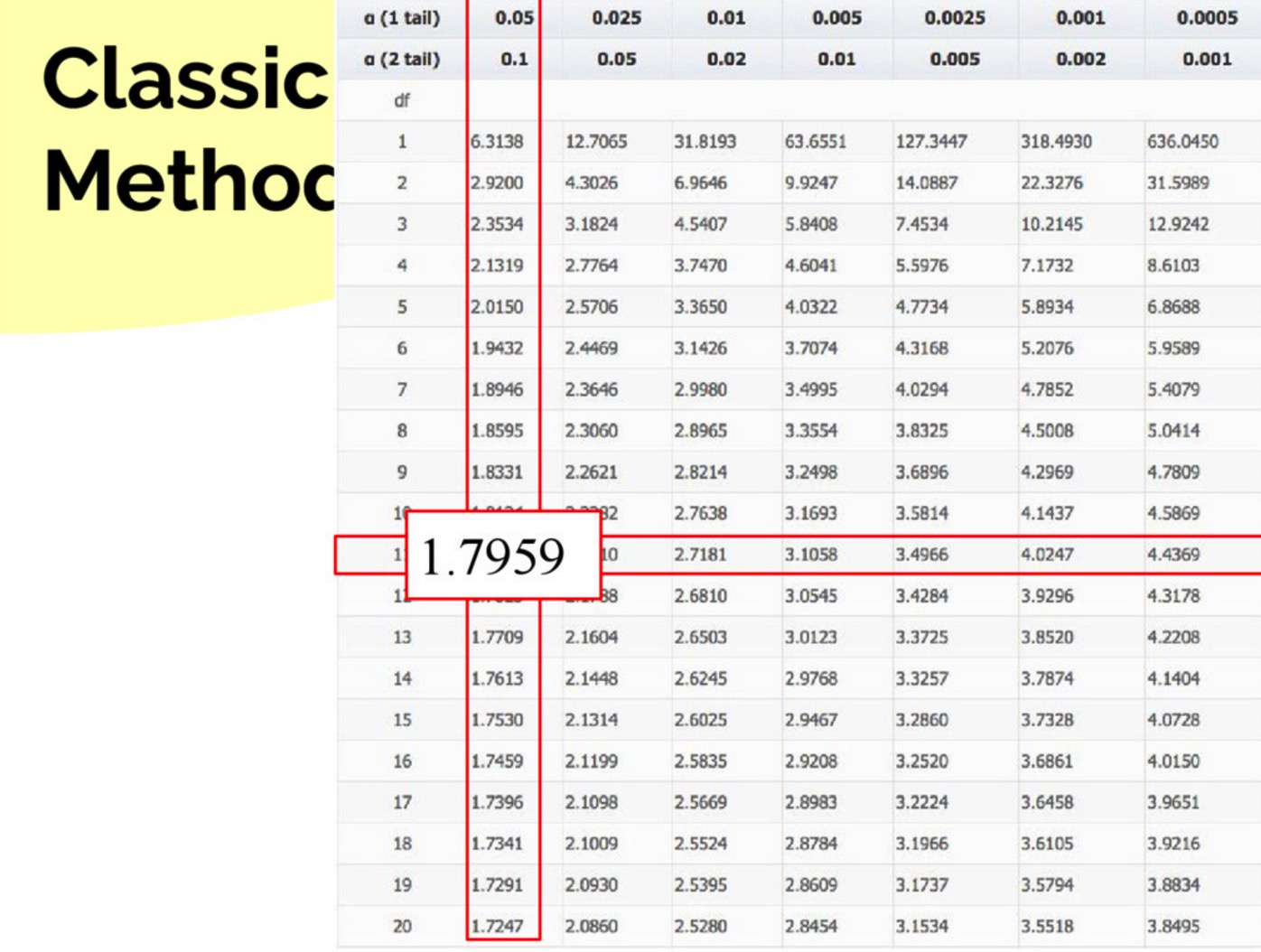
由于 t = 0.932 > tcrit = 1.796，所以我们得到结论：在 p = 0.05 的水平上差异 6.6 不是显著的。

所以……，我们刚刚究竟都做了些什么？最大的问题，是我们在解题过程中已经忘了我们最初要回答的问题。

为什么不直接使用流行的编程方法来处理呢？比如：

from statsmodels.stats.weightstats import ttest_indt, p, dof = ttest_ind(group1, group2,
				alternative='larger',
				usevar='unequal')
print(p)  # 0.186

这当然可以，但是……，我们正尝试回答的是什么问题呢？

让我们回到问题本身，上面的样本分布和抛硬币的原理其实是一样的，让我们用一个抽样方法来处理。和抛硬币不同，这儿我们没有生成器（模拟抛硬币的结果），但这不是问题，我们可以引入一个新的解决方案：随机打乱（Shuffling）。

过程如下图所示：

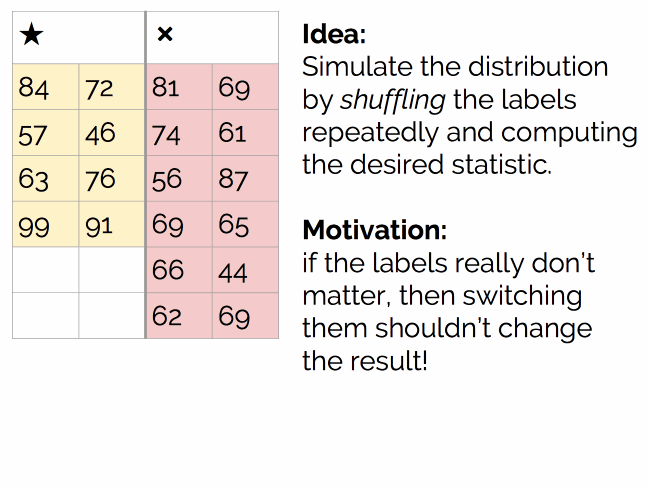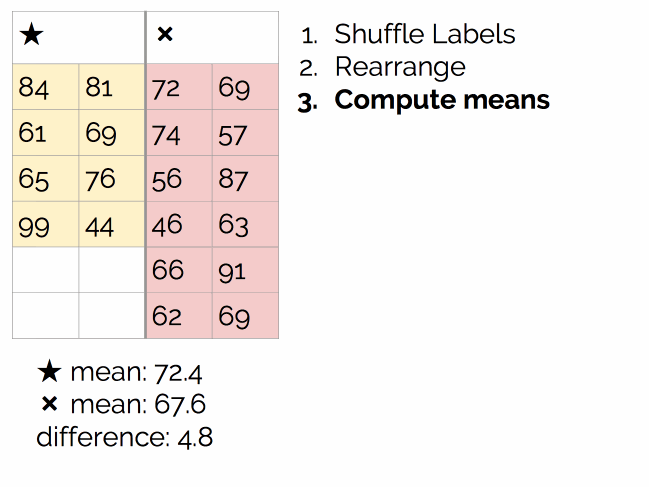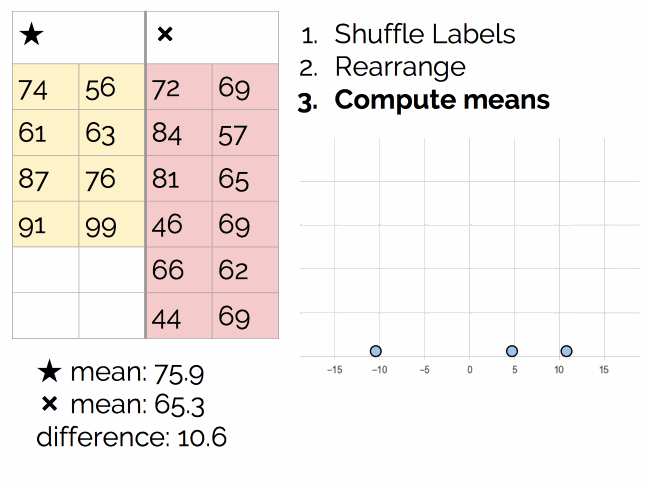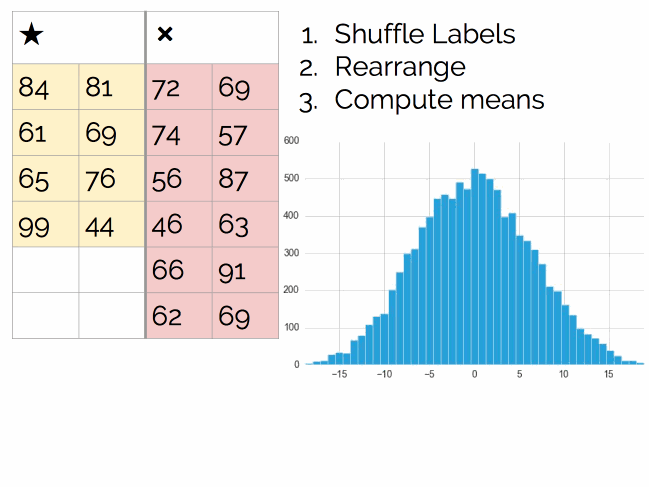
执行数千次，最后得到结论：

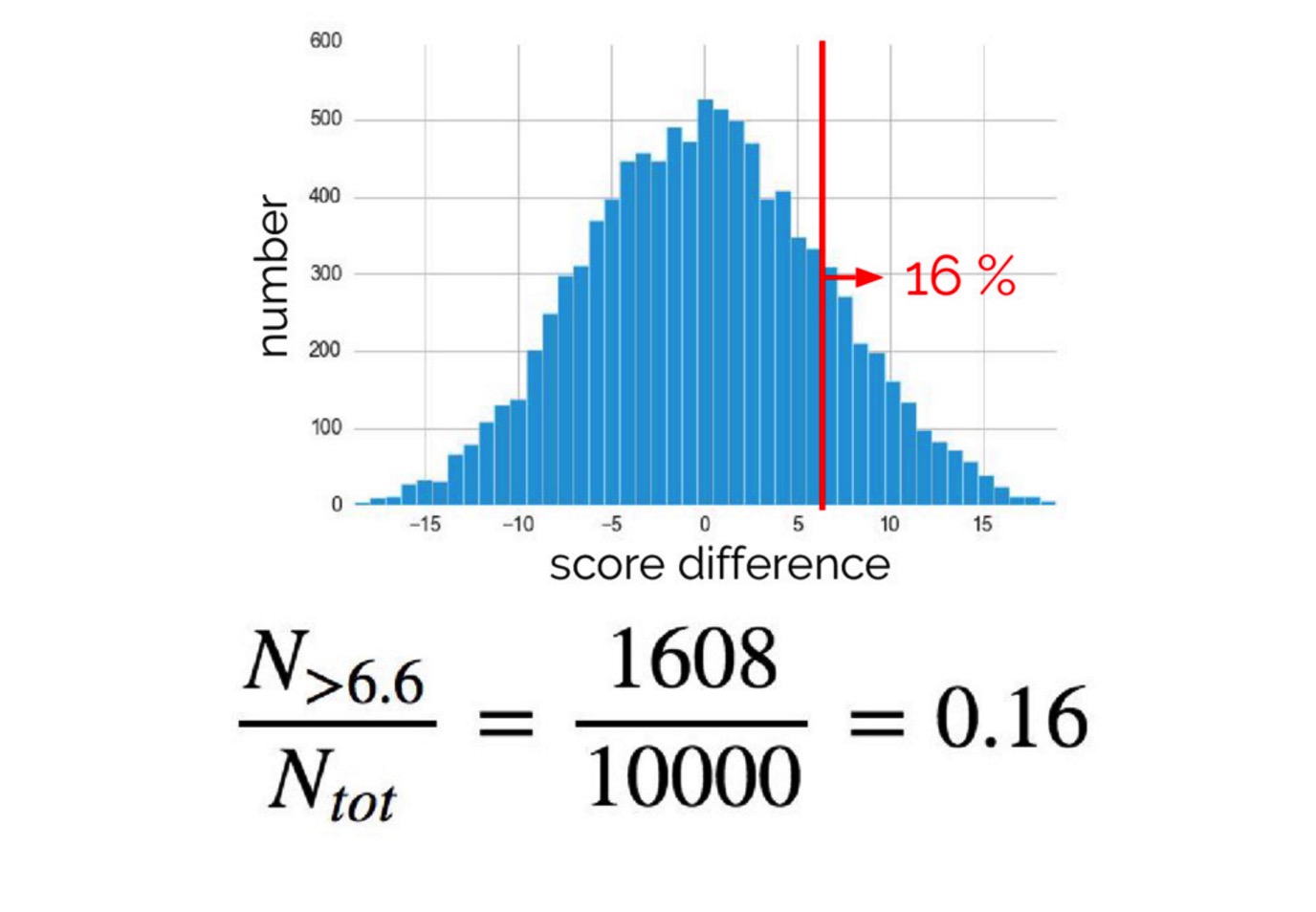
在 p = 0.05 的水平上，差异 6.6 不是显著的。

关于随机打乱需要注意的事：

– 只能在原假设认为两组相同时使用
– 和所有其他方法一样，只能在样本有代表性时使用，千万要注意选择偏差
– 要注意相关实验。这点在《Simon’s Resampling: The New Statistics》一书中有很好的讨论

3. 亚特尔的乌龟塔

亚特尔的乌龟塔是一则童话寓言，讲述的是一只叫亚特尔的乌龟命令其他乌龟叠在一起成为高塔的故事，知名中文博主阮一峰曾经翻译过一个版本。

假设我们观察到了 20 个亚特尔乌龟塔，高度分别为：

48	24	32	61	51	12	32	18	19	24
21	41	29	21	25	23	42	18	23	13

问题是：
– 亚特尔乌龟塔的平均高度是多少？
– 这个估值有多少偏差？

需要注意的是，这儿问的是全体亚特尔乌龟塔的平均高度，即可能存在成千上万个乌龟塔，我们只观察了其中 20 个样本，并对整体均值进行估计，而不是简单地问这 20 个样本的均值，所以才有第二个问题：这个估值有多少偏差。

经典解法如下：

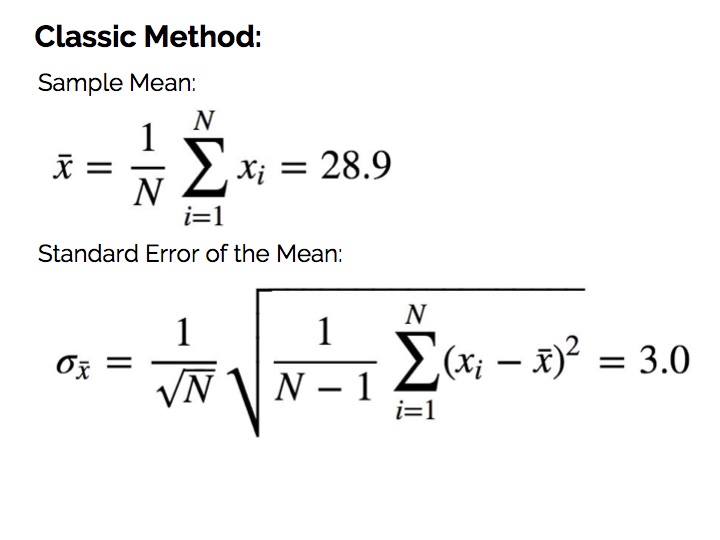
那么，我们是否可以使用抽样方法来处理这个问题呢？和之前一样，我们的问题是没有生成器，这次的解决方案是自助重抽样法（Bootstrap Resampling）。如下图所示：

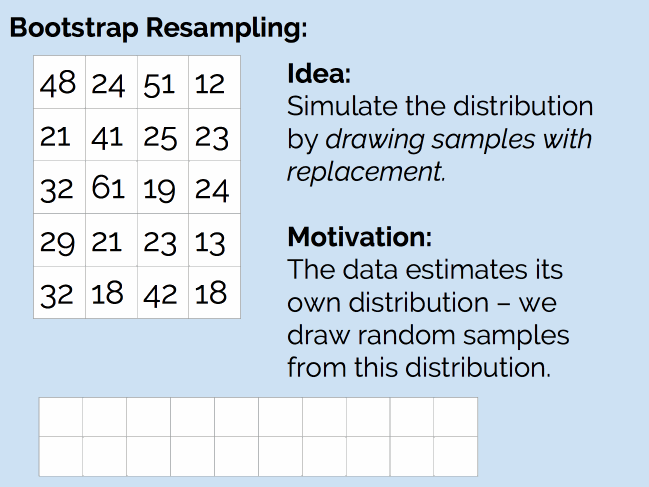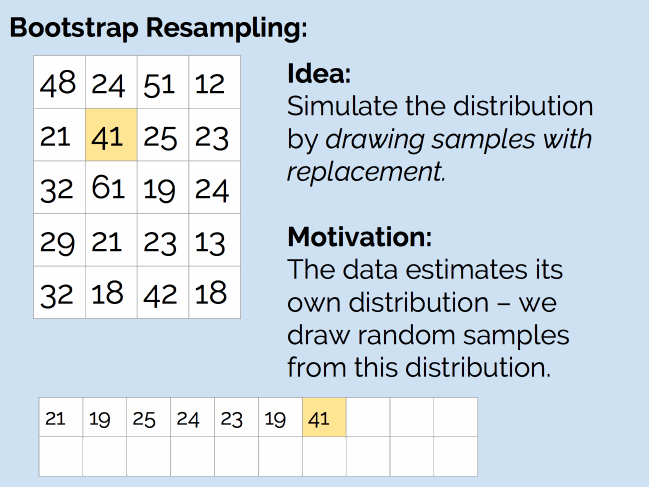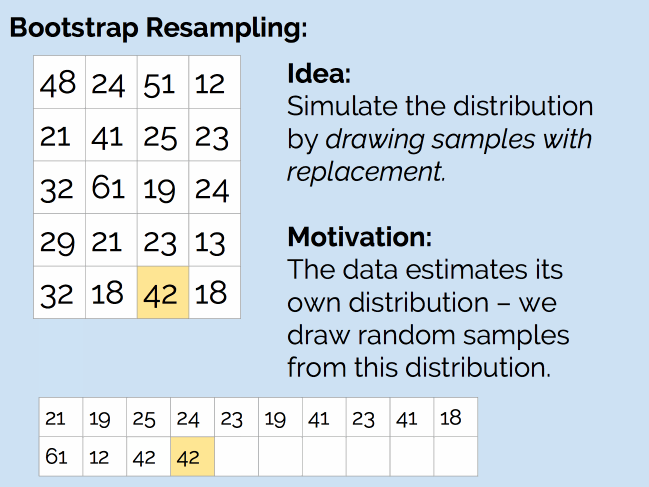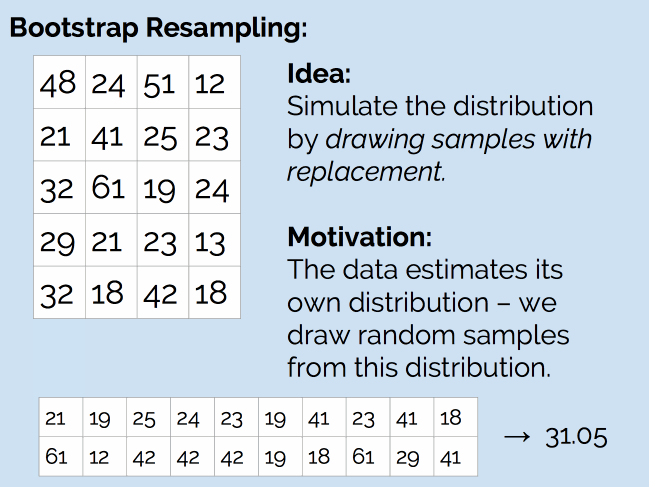
简单来说，就是从现有的 20 个样本中，随机抽取 20 个值（抽完后放回去，因此可能会抽到重复的值），然后计算新样本的均值。

重复这个步骤成千上万次，最后，我们得到下面的结果：

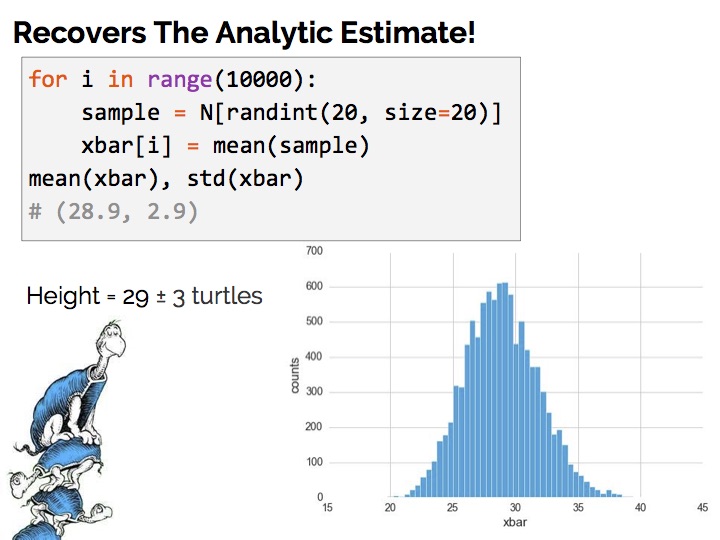
可以看到，与上面使用公式计算出的结果几乎一样。

** 自助重抽样法（Bootstrap Sampling）** 甚至还可以用在更复杂的统计上，同样的，也有一些注意点：

– 自助重抽样法（Bootstrap Sampling）被认真地研究过，有坚实的理论基础
– 自助重抽样法通常不太适用于基于排序的统计（如求最大值）
– 如果样本太小，效果会比较差（N > 20 比较好）
– 注意选择偏差以及非独立数据

4. 交叉验证

最后，PPT 中还举了一个交叉验证的例子。大致思想是将样本随机分为两部分，各自算出需要的值，然后用另一份样本来校验当前样本的值。重复成千上万次，最后得到可信的结果。限于篇幅，这儿就不详细介绍了，有兴趣的同学可以直接看原 PPT。

小结

相对抽象的统计学公式而言，抽样方法是一种更符合直觉的计算近似法。只要会写 for 循环，就可以做统计分析。

参考

《Statistics for Hackers》

1. 热身： 抛硬币问题（直接模拟）

2. 随机打乱

关于随机打乱需要注意的事：

3. 亚特尔的乌龟塔

4. 交叉验证

小结

参考

1. 热身：抛硬币问题（直接模拟）